Today, David and I conducted an interview with Richard Ellis, an astrophysics professor at the California Institute of Technology and my adviser. Professor Ellis didn't require much in the way of guiding questions; he covered a lot on his own, so instead of writing this up in a question-answer format, I'm going to try to write up his stories based on my notes. [I may interject every now and then, but rest assured my statements will be safely walled off behind brackets. Other than that, all that follows should be a paraphrase of Prof. Ellis, as transcribed from my notes. I may write my reflection on the interview in another post]
Tuesday, November 29, 2011
Sunday, November 20, 2011
Water, Water Everywhere
While I was looking things up for my previous post about water on Europa, I ran across this article. It basically summarizes the search for liquid water, both in the solar system and outside it. I haven't looked through the article thoroughly, so I can't really vouch for the accuracy or the up-to-date-ness of its data.
It did, however, remind me of another article that I'd read this past summer:
It did, however, remind me of another article that I'd read this past summer:
A water cloud containing the equivalent of 140 trillion times the water held in Earth's oceans has been detected around a quasar powered by a giant black hole 12 billion light years away.Note that this is water vapor, not liquid water or ice. Also note that this cloud is huge: it spans hundreds of lightyears around a supermassive black hole. Pretty cool.
Europa
Jupiter has 65 satellites, according to the Carnegie Institution for Science. They vary greatly (four of them make up almost all the mass, and Ganymede makes up a third of "almost all" by itself). It is these four, known as the Main Group or the Galilean Moons, that have captured the most interest, perhaps mostly because, as the largest, the are the easiest to see. They are known as the Galilean Moons because they were discovered in 1609 and 1610 by Galileo Galilei, who also famously recorded their orbits around Jupiter, bringing more support to the heliocentric view of the solar system.
As an aside, Galileo originally wanted to name the moons after the four brothers at the head of the powerful Medici family: Cosimo, Francesco, Carlo, and Lorenzo. This idea, though, proved to be less popular outside Florence, leading to the names we know today: Io, Ganymede, Europa, and Callisto, four lovers of the god Zeus in Greek mythology.
Europa, a Galilean moon and the sixth from Jupiter, is a bit smaller than Earth's moon, has a surface made up mostly of silicate rock, and probably has an iron core. It even has a thin atmosphere of oxygen. These and other geological features of the moon have led some to speculate that Europa holds large reserves of subterranean water, possibly entire oceans underground. Because of this, Europa is one of the leading candidates in the solar system for potential habitability and the presence of extraterrestrial life (well, at least since Mars let us down).
Which leads me into this new development. Geophysicists at UT Austin have possibly discovered a large (about the volume of the Great Lakes), surface lake of liquid water on Europa (and by surface, I of course mean several kilometers below the surface). The lake, like much of Europa's surface is mostly obscured by a thick ice shell, and it's not really known what is below it. A large subsurface ocean is one possibility, but another model claims that the top layer, composed of cold and brittle ice, covers a much thicker layer of warmer, convecting ice.
As far as I can tell, this new find doesn't necessarily support either model. This simulation of the formation of the lake seems to ignore that which lies far beneath the surface, instead showing how the lake can form just beneath the top ice sheet. It's possible, though, that I'm not interpreting this correctly.
This certainly isn't enough to get into the idea of actual life on Europa (though apparently some people have even been talking about colonizing it). Liquid water is, however, a step in that direction; it is also just interesting to learn more about the features of our solar system.
As an aside, Galileo originally wanted to name the moons after the four brothers at the head of the powerful Medici family: Cosimo, Francesco, Carlo, and Lorenzo. This idea, though, proved to be less popular outside Florence, leading to the names we know today: Io, Ganymede, Europa, and Callisto, four lovers of the god Zeus in Greek mythology.
Europa, a Galilean moon and the sixth from Jupiter, is a bit smaller than Earth's moon, has a surface made up mostly of silicate rock, and probably has an iron core. It even has a thin atmosphere of oxygen. These and other geological features of the moon have led some to speculate that Europa holds large reserves of subterranean water, possibly entire oceans underground. Because of this, Europa is one of the leading candidates in the solar system for potential habitability and the presence of extraterrestrial life (well, at least since Mars let us down).
Which leads me into this new development. Geophysicists at UT Austin have possibly discovered a large (about the volume of the Great Lakes), surface lake of liquid water on Europa (and by surface, I of course mean several kilometers below the surface). The lake, like much of Europa's surface is mostly obscured by a thick ice shell, and it's not really known what is below it. A large subsurface ocean is one possibility, but another model claims that the top layer, composed of cold and brittle ice, covers a much thicker layer of warmer, convecting ice.
As far as I can tell, this new find doesn't necessarily support either model. This simulation of the formation of the lake seems to ignore that which lies far beneath the surface, instead showing how the lake can form just beneath the top ice sheet. It's possible, though, that I'm not interpreting this correctly.
This certainly isn't enough to get into the idea of actual life on Europa (though apparently some people have even been talking about colonizing it). Liquid water is, however, a step in that direction; it is also just interesting to learn more about the features of our solar system.
Tuesday, November 15, 2011
Stars and the Virial Theorem
The Virial Theorem is a theorem in mechanics that relates the kinetic energy of particles in a system to the potential of the system. This can be useful when talking about stars, which balance both an immense gravitational collapsing force from their huge mass with the outward force from the internal particles heated from fusion at the star's core.
Sunday, November 13, 2011
Wednesday, November 9, 2011
Happy Birthday, Carl Sagan
Today would be Carl Sagan's 77th birthday. He was an American astronomer and popular science writer, known for such works as Cosmos, The Demon Haunted World, and the novel Contact, which was later adapted into a film. But my personal favorite book of his is Pale Blue Dot, from which the above speech was taken. He is referencing this picture:
 |
| Picture from www.realscience.us |
 |
| Picture from Wikipedia |
This one was taken by Apollo 8 crewmember Bill Anders, on December 24, 1968.
The Initial Mass Function II: The Luminosity Strikes Back
Continuing the problem from the previous post (and ignoring the lame Star Wars reference), we now have 3 mass categories of stars in the cluster, and the total masses contained in each of these categories in the cluster.
Now suppose we want to find the total luminosity of the cluster. If the luminosity scaled with mass the same way for all masses of stars, then this would be easy. We could just use the total mass and convert it to luminosity using that relation.
It's not quite that simple, though, which is why in the previous post it was necessary to break the stars into categories: different masses of stars have different mass-luminosity relations. Here they are for low, intermediate, and high mass stars, respectively:
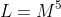
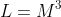
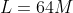
So, with each of the masses calculated in the previous post, we can use each of these relations to find the total luminosity for each category. The sum of these will be the total luminosity of the cluster.
I left those masses in terms of the solar mass, so finding the luminosity in erg/s will take some calculation. Help me, WolframAlpha, you are my only hope...
Once the luminosities are found, one can use them and Wien's Displacement Law to find the maximum-intensity wavelengths of the stars. Because younger stars are generally more luminous than older ones (they have more fuel which they use more wuickly), the average output radiation will be toward the blue end of the spectrum; older, cooler stars tend to be red.
Now suppose we want to find the total luminosity of the cluster. If the luminosity scaled with mass the same way for all masses of stars, then this would be easy. We could just use the total mass and convert it to luminosity using that relation.
It's not quite that simple, though, which is why in the previous post it was necessary to break the stars into categories: different masses of stars have different mass-luminosity relations. Here they are for low, intermediate, and high mass stars, respectively:
So, with each of the masses calculated in the previous post, we can use each of these relations to find the total luminosity for each category. The sum of these will be the total luminosity of the cluster.
I left those masses in terms of the solar mass, so finding the luminosity in erg/s will take some calculation. Help me, WolframAlpha, you are my only hope...
Once the luminosities are found, one can use them and Wien's Displacement Law to find the maximum-intensity wavelengths of the stars. Because younger stars are generally more luminous than older ones (they have more fuel which they use more wuickly), the average output radiation will be toward the blue end of the spectrum; older, cooler stars tend to be red.
Tuesday, November 8, 2011
The Initial Mass Function
The Initial Mass Function describes the mass distribution of a population of stars based on their theoretical initial masses (the masses they had at "birth"). The IMF is an empirically derived function; ie, it has been found to be true in numerous actual sets of stars, and was derived from that data, rather than being theoretically predicted. The IMF has this form:

where N is the number of stars, M is the mass of a star, and A is a proportionality constant.
Suppose we have discovered a newly formed globular cluster with a total mass of a million solar masses, and the masses of the stars it contains range from .1 solar masses to 20 solar masses. What can we find out about the cluster given this information?
First, we ought to find A. The first step is to integrate, so we have N as a function of M. (And we'll be playing a little fast and loose with the rules of differential equations, so don't hate me, mathematicians.)

from one tenth of a solar mass to 20 solar masses. Don't get too hung up on the limits of integration, because we'll be integrating again right away. This will give us the total mass of the system, which, fortunately, we know:
![\bg_white M_T=10^6M_S=\int NdM=\frac{-A}{1.35}\int_{.1M_S}^{20M_S}M^-^1^.^3^5dM=\frac{-A}{(1.35)(-.35)}[(\frac{1}{20M_S})^.^3^5-(\frac{1}{.1M_S})^.^3^5]](http://latex.codecogs.com/gif.latex?\bg_white M_T=10^6M_S=\int NdM=\frac{-A}{1.35}\int_{.1M_S}^{20M_S}M^-^1^.^3^5dM=\frac{-A}{(1.35)(-.35)}[(\frac{1}{20M_S})^.^3^5-(\frac{1}{.1M_S})^.^3^5])
Substituting in the values for the variables (and rounding a bit, and approximating), we get
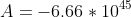
Cool. Now, suppose we divide the stars into categories: massive (between 8 and 20 solar masses), intermediate (between 1 and 8 solar masses) and low-mass (between .1 and 1 solar masses).What is the fraction of total stars in the cluster from each of these categories?
First, we can find the total number in each category. Now that we have the value of A, we can use the first integral above (where we found N as a function of M), except changing the limits of integration to be one of the sets of boundaries for a mass category (eg, 8 masses to 20 masses for massive stars). Solving these integrals gives around 3540 massive stars, 77,600 intermediate stars, and 1,767,000 low-mass stars. This makes massive stars about .2 % of the cluster by number, intermediate stars about 4.2 %, and low-mass stars 95.6 %.
One can also find the total mass contained in each of these categories in this particular cluster by using similar limits on the second integral. This gives about 75,000 solar masses; 280,000 solar masses; and 650,000 solar masses, respectively.
I will continue discussing the Initial Mass Function in a second post, covering more of this problem.
Worked out with Mee and David.
where N is the number of stars, M is the mass of a star, and A is a proportionality constant.
Suppose we have discovered a newly formed globular cluster with a total mass of a million solar masses, and the masses of the stars it contains range from .1 solar masses to 20 solar masses. What can we find out about the cluster given this information?
First, we ought to find A. The first step is to integrate, so we have N as a function of M. (And we'll be playing a little fast and loose with the rules of differential equations, so don't hate me, mathematicians.)
from one tenth of a solar mass to 20 solar masses. Don't get too hung up on the limits of integration, because we'll be integrating again right away. This will give us the total mass of the system, which, fortunately, we know:
Substituting in the values for the variables (and rounding a bit, and approximating), we get
Cool. Now, suppose we divide the stars into categories: massive (between 8 and 20 solar masses), intermediate (between 1 and 8 solar masses) and low-mass (between .1 and 1 solar masses).What is the fraction of total stars in the cluster from each of these categories?
First, we can find the total number in each category. Now that we have the value of A, we can use the first integral above (where we found N as a function of M), except changing the limits of integration to be one of the sets of boundaries for a mass category (eg, 8 masses to 20 masses for massive stars). Solving these integrals gives around 3540 massive stars, 77,600 intermediate stars, and 1,767,000 low-mass stars. This makes massive stars about .2 % of the cluster by number, intermediate stars about 4.2 %, and low-mass stars 95.6 %.
One can also find the total mass contained in each of these categories in this particular cluster by using similar limits on the second integral. This gives about 75,000 solar masses; 280,000 solar masses; and 650,000 solar masses, respectively.
I will continue discussing the Initial Mass Function in a second post, covering more of this problem.
Worked out with Mee and David.
Monday, November 7, 2011
Professional Astronomy
"The primary mission of our department is twofold: the performance of cutting-edge research in astronomy and astrophysics, including theory, observation, and experiment, as well as the education of undergraduate and graduate students and training of postdoctoral research associates who will comprise the scientists and leaders of tomorrow."This is how the Caltech Astronomy Department defines its purpose, as given on its website. This is, of course, a pretty broad definition, so it can include a lot of different people doing a lot of different things. Furthermore, the teaching faculty page breaks down the astrophysics faculty into theoretical, observational, and experimental astrophysicists; each may encompass a different aspect of what astronomers do (though the more literal-minded among us may consider only observational astrophysics to "really" be astronomy).
So, if one defines a professional astronomer as a person who has a faculty position in astrophysics, the above definition may be pretty sound. But this is not the only avenue for astronomy. For example, I did research this summer with scientists at the Spitzer Science Center. Though the Center is affiliated with and on the campus of Caltech, the people who do research there are not professors; they do not teach courses. So one can be an astronomer outside of (albeit still close to) academia.
The only astronomy research I am personally familiar with is observational. Last summer, as I've mentioned before, I used data from bright, infrared galaxies to draw conclusions about infrared power sources. And a year before that, I used photometry to calculate the rotational periods of asteroids. As a result, I don't really know much about the more theoretical side of astronomy. Learning more about that is one of my main goals for my time here at Caltech.
Monday, October 31, 2011
Happy Halloween
It's a ghost!
This is actually known as the Ghost of the Cepheus Flare. The Cepheus Flare is a molecular cloud about 1200 lightyears away. This "ghost" is actually a 2-lightyear-wide dust cloud at the very edge of the flare, seen by reflected starlight. The bulges in the cloud's shape are nebula regions; the section of dust on the far right of the image is collapsing in on itself, and is likely in the first stages of forming a binary star.
This is actually known as the Ghost of the Cepheus Flare. The Cepheus Flare is a molecular cloud about 1200 lightyears away. This "ghost" is actually a 2-lightyear-wide dust cloud at the very edge of the flare, seen by reflected starlight. The bulges in the cloud's shape are nebula regions; the section of dust on the far right of the image is collapsing in on itself, and is likely in the first stages of forming a binary star.
Can You See the Seahorse?
Above is a picture of a seahorse in the Large Magellanic Cloud, a nearby satellite galaxy of the Milky Way. What looks to us like a seahorse (an example of pareidolia, the same phenomenon that lets us see constellations in groups of stars and the man in the moon) is actually a pillar of dust 20 lightyears long.
The seahorse is very close to another well-known object in the LMC, the Tarantula Nebula:
The Tarantula Nebula is very energetic, and is in the process of forming a star cluster, the center of which is just above the cutoff of the Seahorse image. As stars form in the cluster, the resulting solar wind will slowly erode the Seahorse dust pillars over the next million years or so.
I think it is often pictures like this that first get people interested in astronomy. There are several reasons for this. The first is rather obvious: they look really cool. Pictures of astronomical objects can be really artistic, and sometimes breathtaking in their patterns and complexity. This can be enhanced when one is able to see something familiar in the picture, like the Magellanic Cloud's Seahorse.
But then there's another dimension. It's fun to imagine a seahorse in the picture, but it's even more interesting to learn what the image really is. A towering pillar of smoky dust, billowing and reforming as the nearby nebula grows and grasps it ever more tightly. It's a monument taller than the highest skyscraper we will ever build, and it's over 150,000 lightyears away, a distance greater than we could possibly imagine. Yet through the technology of the Hubble Telescope, we are able to gaze into the deep, dark night, and find a seahorse sculpted by gravity and eons.
Tuesday, October 25, 2011
Nuclear Winter
So, in Battlestar Galactica, the Cylons have just launched a nuclear attack on the Twelve Colonies, including the Earth-like world of Caprica. This is, of course, terribly sad, but we will assuage our grief with science.
Each bomb the Cylons use kicks up a lot of dust into the planet's atmosphere. And increasing the amount of optically thick dust in the atmosphere reduces the sunlight that reaches the planet's surface, which results in lower surface temperatures. Can we figure out the relationship between the amount of dust in the atmosphere and the cooling of the surface?
OK, so suppose the Cylons drop N bombs, and each bomb moves a mass M of dust into the atmosphere. Each dust particle has a a mass density rho and a radius r (assume a spherical dust particle).
First, we should find the total number of particles moved to the atmosphere. Note that
where mp is the mass per particle and Vp is the volume per particle. So we can write
where the units of mp are kg/particle. NM is the total mass of particles. So if we take
we have units of particles, so Np is the total number of particles.
Next we need to find the fraction of flux that gets through the dust and to the planet's surface. We'll assume that
is the surface area of a particle of dust, and
is the surface area of the planet, with R being comparable to the Earth's radius. So then we have
for the ratio of the flux that reaches the planet's surface to the flux that reaches the planet. Since temperature is related to flux by
we can find the factor relating the original temperature to the new with
The only problem with this formulation is with the flux ratio. When the second term is greater than one, which occurs for large numbers of bombs or masses of dust, the result is a negative ratio, which doesn't make sense.
Worked out with David and Mee.
Also, on a semi-related note, if you are a fan of nuclear winter and/or post-apocalyptic fiction, I recommend The Road by Cormac McCarthy.
Monday, October 24, 2011
The Big Bang
If you watch the TV show "The Big Bang Theory," you may be somewhat familiar with this song.
One quibble, though. The members of the band Barenaked Ladies appear to be proponents of the Big Crunch hypothesis for the Ultimate Fate of the Universe, but all current evidence shows that the universe is not only expanding, but accelerating in its expansion. So, if things keep going the way they are, the universe won't reconstitute itself into a singularity, but will keep expanding outward. Most of the universe will move so far away so fast the it will pass beyond our local event horizon (its light won't be able to reach us because it is expanding away too quickly).
The most commonly held hypothesis for the fate of the universe is the Big Freeze, or heat death. This occurs when the universe achieves maximum entropy, leaving the universe bereft of free energy capable of doing work. Sadly, this would put an end to most of the interesting parts of the universe.
That could be a bit depressing, so let's end with something more optimistic:
Wednesday, October 19, 2011
The Distance to the Sun
The above image is a series of pictures of Mercury passing between the Earth and the Sun. It was taken from a satellite in polar orbit around the Earth. Is there any way we can use information from this picture, and some other basic astronomy knowledge, to find the distance from the Earth to the Sun?
The above diagram can help us find everything we need to know. We want to find a, a variable that stands for the astronomical unit, or the distance from the Earth to the Sun. Supposing we have only the orbital periods of the Earth and Mercury, and the two pictures above, can we find it? Kepler's Laws and trigonometry say yes.
First, we can use the picture of Mercury's motion to find the angle alpha in the upper left of the diagram. If you look at the picture, you may notice that Mercury's "height" relative to the Sun oscillates up and down. This is due to the movement of the satellite around the Earth: when it's near the North Pole, Mercury's position relative to the Sun appears different compared to when viewed from the South Pole. The angle between Mercury's high and low points is alpha.
We know that the height of the Sun (the diameter) is 0.5 degrees relative to the total sky. By comparing Mercury to the Sun in the above picture, one can estimate Mercury's oscillation in degrees. It's not very big: about 0.0005 degrees. This is alpha. In radians, alpha is 0.00000876.
OK, what next? Take a look at the top triangle, whose angles are alpha, beta, and pi minus theta. Since the sum of these angles is equal to pi (using radians), we have
Using trigonometry and small-angle approximations, we have
Solving for delta-a, we get
Since the total distance a is the sum of delta-a and the distance from Mercury to the Sun, we can write
So, how does this help us? Fortunately, Kepler's Third Law of Planetary Motion says that the square of a planet's orbital period is proportional to the cube of the planet's semimajor axis, which we call a. So we have
We know the radius of the Earth (using 6300 km), and that the Earth's orbital period is 365 days, so if we also happen to know that Mercury's orbital period is 87 days, we can solve for a. Though I must warn you, it involves some pretty hideous algebra. Do not attempt at home.
But, if you do, you get around 200 million kilometers. How much is it really? About 150 million kilometers. Cool.
Given this, we can use a refined version of Kepler's Third law to find the mass of the Sun:
Assuming we're using Earth, we know everything in this equation now except for the mass of the Sun (We can neglect the Earth's mass, as it is ridiculously tiny compared to that of the Sun). Using the values we've calculated, I get
for the mass of the Sun. What is it really?
So we end up a bit under on our estimate, coming up with only about 30% of the mass of the Sun.
Worked on with Mee and David.
Tuesday, October 18, 2011
Friday, October 14, 2011
More on Blackbodies
Previously on Looking Up, we explored the Blackbody properties of a Y Dwarf orbiting a Sun-like star, and we found the peak wavelength emitted by the Y Dwarf given its temperature. From this, we were able to calculate the photons per second per area from the Y Dwarf that reached an observer 30 lightyears away. But many questions were left unanswered: how many photons came from the Sun-like star? What is the flux ratio of the Y Dwarf to this star? Tonight, the thrilling conclusion:
Thursday, October 13, 2011
Blackbody Radiation
Anything with a temperature above absolute 0 (which, considering that the background temperature of space is 2.7 K, is pretty much everything) emits lights with varying degrees of efficiency. Stars, for instance, are some of the most efficient emitters. Ideal emitters (an object that absorbs all light energy that hits it and reradiates that energy in a certain spectrum) reflect no light, and are thus known as blackbodies, and the reradiated energy is called blackbody radiation. Stars are not actually ideal emitters, but they are close enough to roughly approximate one. Some example blackbody spectra are shown on this graph:
As you can see from this graph, the blackbody spectrum varies with temperature. If you want to see an example of some of the things you can do with this fact, keep reading.
As you can see from this graph, the blackbody spectrum varies with temperature. If you want to see an example of some of the things you can do with this fact, keep reading.
Monday, October 10, 2011
Universe Sandbox
I recently purchased a program called Universe Sandbox for $5. It is billed as an interactive space gravity simulator, featuring much of the known universe. You can focus on the solar system, nearby stars, the Milky Way, even the Local Cluster. You can click on each major object, and it will provide you with a list of pertinent information: mass, density, radius, orbit eccentricity, etc. That's cool, but it's not the best part. Having selected the pertinent information, you are then free to change it and see what happens!
Pretty much nothing is off-limits, not even the gravitational constant. You can add moons, or take them away. You can build your own solar system from scratch, or mess with the one we have. It's pretty awesome.
The program also can save screenshots, so I'll post images here if I discover anything interesting. So far, the main thing I've learned is that if you increase the radius of the Sun by a factor of 100, the Earth will die a fiery death. But that's not too surprising, so in the meantime, here's a simulation of the collision of the Milky Way and the Andromeda Galaxy.
It's due to happen in 4.5 billion years. Mark your calendars.
Pretty much nothing is off-limits, not even the gravitational constant. You can add moons, or take them away. You can build your own solar system from scratch, or mess with the one we have. It's pretty awesome.
The program also can save screenshots, so I'll post images here if I discover anything interesting. So far, the main thing I've learned is that if you increase the radius of the Sun by a factor of 100, the Earth will die a fiery death. But that's not too surprising, so in the meantime, here's a simulation of the collision of the Milky Way and the Andromeda Galaxy.
It's due to happen in 4.5 billion years. Mark your calendars.
More on ULIRGs
My presentation on my research is coming up, and there were some questions after my first post, so I thought I'd elaborate.
Saturday, October 8, 2011
Astronomy at the Beach
This post is a little overdue, as this experiment occurred last week, but whatever. Last Friday, most of the Ay 20 class journeyed to Santa Monica beach, not merely for the cool ocean breeze or the calming sound of waves breaking on the sand, but for science. Read on for the details.
Wednesday, October 5, 2011
Eric Idle and Astronomy
If you haven't seen Monty Python's The Meaning of Life, I highly recommend it.
Tau Ceti and Declination
Partners: Nathan, Mee, Eric
Imagine you are standing outside on a clear night, far away from any sources of light pollution, yet also in the relative vicinity of Palomar Observatory (this will be important later). When you look up, you see a vast array of stars spread out before you.
Now, before you get too distracted by the splendor of the night sky, turn to face north, and find Polaris. Polaris is the North Star, and it is fixed in the heavens (for the next several thousand years, anyway), shining above the northern horizon.
If you watched the area around Polaris for the whole night, you would see the sky appear to rotate around it, with the paths of nearby stars tracing (parts of) circles in the night around the unmoving North Star.
You see, the Earth’s axis of rotation points toward Polaris; therefore, as the Earth rotates during the night, the angle between Polaris, the point of observation, and the observed star changes. So the star in question appears to be at a different point in the sky.
If you shift your observation of the sky to a position south of the area around Polaris, you’ll notice that the stars in this area trace larger circles. If you were able to watch their paths for 24 hours (the Sun tends to be a problem here), you would perhaps see that part of the stars’ paths are blocked by the Earth; their movements take place “behind” the horizon.
Why do the paths get longer as your gaze drifts south? This is a function of declination. This is essentially the same as latitude, and is measured in degrees north or south of the celestial equator (the celestial equator is simply the plane of the Earth’s equator extended out into space). Palomar is at about 30 degrees North; any object directly above it in the sky will have a declination of 30 degrees N (or an object directly above any point on the 30-degree latitude line).
You can also think of the declination as an angle whose vertex is at the Earth’s center, with one line on the celestial equator and one connecting the center of the Earth to the star in question. So Polaris, on the line of Earth’s rotational axis, is perpendicular to the celestial equator. Thus, Polaris’ declination is 90 degrees.
Take another star, Tau Ceti. It has a declination of negative 15 degrees, so it is in the Southern Hemisphere. But it’s close enough to the declination of the equator (0 degrees) that it should be visible in parts of the Northern Hemisphere. Like, say, Palomar.
Suppose that from Palomar’s 30 degrees N, any object with a declination >30 degrees is visible in the sky throughout the day. Everything between -30 and 30 is visible at some times but not others. Everything below -30 is never seen in the sky above Palomar.
Tau Ceti is within the sometimes-visible interval. So, when can we see Tau Ceti? Well, obviously we can’t see it during the day, because there’s an annoyingly close star whose light masks the presence of other stars during the daytime. At this latitude, the Sun is visible for just over 14 ours at the summer solstice, and just over 10 at the winter. Give it an extra two hours for the sky to darken, and you have possibly eight hours of time to see Tau Ceti in the summer and 12 in the winter.
But there is another factor to consider here. As the Earth moves in its orbit around the Sun, the time at which an object reaches the meridian (the highest point it reaches in the sky, and the best point for viewing) changes. Because, when the Earth rotates, it takes 360 degrees to complete one full rotation. But because it is also moving in space, after one full rotation, it must then rotate one extra degree to bring the starting point of the measurement in line with the sun. This extra rotation takes about 4 minutes. Accordingly, a given distant star will rise 4 minutes earlier each subsequent night.
Tau Ceti’s Right Ascension is 1 hour and 44 minutes, so about 2 hours. This is the time after noon (set at 0:00 hours) that a star will reach the meridian in the sky on the Vernal Equinox (known by some as March 20). So in late March, Tau Seti will be in prime viewing position around 2 pm. This is obviously a problem, as the Sun is also in prime viewing position around 2 pm. So when will Tau Ceti peak at a better time?
Every 30 days is about 120 minutes of change, or 2 hours. So around April 20, Tau Ceti will peak around noon. Not better. But by August, it will be peaking at around 4 in the morning. Tau Ceti will reach meridian at midnight in October.
So, if we assume that, because of its declination, Tau Ceti is best viewed around its meridian peak, when it can’t be hidden by the horizon, and that Tau Ceti, like most stars, is best viewed at night, then we can estimate the best times for viewing Tau Ceti as early fall to early winter.
Possibly more to follow, including graphs, if I have time.
Imagine you are standing outside on a clear night, far away from any sources of light pollution, yet also in the relative vicinity of Palomar Observatory (this will be important later). When you look up, you see a vast array of stars spread out before you.
Now, before you get too distracted by the splendor of the night sky, turn to face north, and find Polaris. Polaris is the North Star, and it is fixed in the heavens (for the next several thousand years, anyway), shining above the northern horizon.
If you watched the area around Polaris for the whole night, you would see the sky appear to rotate around it, with the paths of nearby stars tracing (parts of) circles in the night around the unmoving North Star.
You see, the Earth’s axis of rotation points toward Polaris; therefore, as the Earth rotates during the night, the angle between Polaris, the point of observation, and the observed star changes. So the star in question appears to be at a different point in the sky.
If you shift your observation of the sky to a position south of the area around Polaris, you’ll notice that the stars in this area trace larger circles. If you were able to watch their paths for 24 hours (the Sun tends to be a problem here), you would perhaps see that part of the stars’ paths are blocked by the Earth; their movements take place “behind” the horizon.
Why do the paths get longer as your gaze drifts south? This is a function of declination. This is essentially the same as latitude, and is measured in degrees north or south of the celestial equator (the celestial equator is simply the plane of the Earth’s equator extended out into space). Palomar is at about 30 degrees North; any object directly above it in the sky will have a declination of 30 degrees N (or an object directly above any point on the 30-degree latitude line).
You can also think of the declination as an angle whose vertex is at the Earth’s center, with one line on the celestial equator and one connecting the center of the Earth to the star in question. So Polaris, on the line of Earth’s rotational axis, is perpendicular to the celestial equator. Thus, Polaris’ declination is 90 degrees.
Take another star, Tau Ceti. It has a declination of negative 15 degrees, so it is in the Southern Hemisphere. But it’s close enough to the declination of the equator (0 degrees) that it should be visible in parts of the Northern Hemisphere. Like, say, Palomar.
Suppose that from Palomar’s 30 degrees N, any object with a declination >30 degrees is visible in the sky throughout the day. Everything between -30 and 30 is visible at some times but not others. Everything below -30 is never seen in the sky above Palomar.
Tau Ceti is within the sometimes-visible interval. So, when can we see Tau Ceti? Well, obviously we can’t see it during the day, because there’s an annoyingly close star whose light masks the presence of other stars during the daytime. At this latitude, the Sun is visible for just over 14 ours at the summer solstice, and just over 10 at the winter. Give it an extra two hours for the sky to darken, and you have possibly eight hours of time to see Tau Ceti in the summer and 12 in the winter.
But there is another factor to consider here. As the Earth moves in its orbit around the Sun, the time at which an object reaches the meridian (the highest point it reaches in the sky, and the best point for viewing) changes. Because, when the Earth rotates, it takes 360 degrees to complete one full rotation. But because it is also moving in space, after one full rotation, it must then rotate one extra degree to bring the starting point of the measurement in line with the sun. This extra rotation takes about 4 minutes. Accordingly, a given distant star will rise 4 minutes earlier each subsequent night.
Tau Ceti’s Right Ascension is 1 hour and 44 minutes, so about 2 hours. This is the time after noon (set at 0:00 hours) that a star will reach the meridian in the sky on the Vernal Equinox (known by some as March 20). So in late March, Tau Seti will be in prime viewing position around 2 pm. This is obviously a problem, as the Sun is also in prime viewing position around 2 pm. So when will Tau Ceti peak at a better time?
Every 30 days is about 120 minutes of change, or 2 hours. So around April 20, Tau Ceti will peak around noon. Not better. But by August, it will be peaking at around 4 in the morning. Tau Ceti will reach meridian at midnight in October.
So, if we assume that, because of its declination, Tau Ceti is best viewed around its meridian peak, when it can’t be hidden by the horizon, and that Tau Ceti, like most stars, is best viewed at night, then we can estimate the best times for viewing Tau Ceti as early fall to early winter.
Possibly more to follow, including graphs, if I have time.
Sunday, October 2, 2011
Supermassive Black Hole
I mentioned supermassive black holes briefly in my last post as one of the potential causes of the power outputs of ultraluminous galaxies. However, I don't actually know a lot about them, so I went to my favorite place for quick information, Wikipedia.
http://en.wikipedia.org/wiki/Supermassive_black_hole
According to this esteemed database (don't worry, the article appears to be properly referenced), while stellar black holes have masses on the order of those of large stars (makes sense), supermassive black holes may have millions of solar masses. More interesting, though, is the claim about the density of supermassive black holes:
The average density of a supermassive black hole (defined as the mass of the black hole divided by the volume within its Schwarzschild radius) can be much less than the density of water (the densities are similar for 108 solar mass black holes[5]). This is because the Schwarzschild radius is directly proportional to mass, while density is inversely proportional to the volume. Since the volume of a spherical object (such as the event horizon of a non-rotating black hole) is directly proportional to the cube of the radius, average density decreases for larger black holes, being inversely proportional to the square of the mass.The Schwarzchild radius is the distance from the center of an object such that, if an object's total mass is contained within the sphere of the Schwarzchild radius, the necessary escape velocity would be the speed of light. Which, unless you are some sort of rule-breaking neutrino, is against the law.
A black hole occurs when the radius of the object is less than that of its Schwarzchild radius. Fortunately for us, most things (like, say, the Milky Way) are not so compact.
But, the larger the Schwarzchild radius, the less compact (ie, dense) and object needs to be to still fulfill the criteria to be a black hole. And since the Schwarzchild radius is proportional to mass, the more massive an object, the less dense it needs to be. Wow.
Further links in case you're interested.
Tuesday, September 27, 2011
Looking Up
The title of this post, and of my blog, comes from this talk by astronomer Neil DeGrasse Tyson, in which he defends the importance of maintaining the space program. It is important, he says, for people to start "looking up," to realize that there is so much more out there than the things people worry about day to day.
I don't mean to inflate the importance of astronomy, or to belittle the real and significant problems facing the world today. The point, I think, is that discovery is never a waste of time.
For example, I did research at Caltech over the summer, and I'll be the first to admit that I don't think my results have any practical value. But I (and hopefully you!) don't see it as a waste of time.
I did work studying Ultraluminous Infrared Galaxies (or ULIRGs), objects emitting over a trillion times the luminescence of the sun, mostly in the infrared (as you may have guessed). This huge radiation output is generally the result of two things: the accretion of mass by a galaxy's central, supermassive black hole, or the widespread formation of new stars. Both of these phenomena are often caused by merging systems; that is, this is what happens when galaxies run into each other at top speed. Awesome.
The graph is the result of a program that breaks down the emission spectrum into several sources, including stellar light and various temperatures of dust. A galaxy powered by a black hole results in a different decomposed spectrum than one mostly powered by star formation.
Now, this sort of information has pretty much no impact on everyday life. I don't really see how it could. But we don't seek to learn only to solve the problems standing immediately before us, but also to drive a process of discovery that I think enriches society. Literature won't feed the hungry, but surely there is no doubt of its cultural value. A value that is, I think, similar to that of looking up.
Subscribe to:
Comments (Atom)






