Today, David and I conducted an interview with Richard Ellis, an astrophysics professor at the California Institute of Technology and my adviser. Professor Ellis didn't require much in the way of guiding questions; he covered a lot on his own, so instead of writing this up in a question-answer format, I'm going to try to write up his stories based on my notes. [I may interject every now and then, but rest assured my statements will be safely walled off behind brackets. Other than that, all that follows should be a paraphrase of Prof. Ellis, as transcribed from my notes. I may write my reflection on the interview in another post]
Tuesday, November 29, 2011
Sunday, November 20, 2011
Water, Water Everywhere
While I was looking things up for my previous post about water on Europa, I ran across this article. It basically summarizes the search for liquid water, both in the solar system and outside it. I haven't looked through the article thoroughly, so I can't really vouch for the accuracy or the up-to-date-ness of its data.
It did, however, remind me of another article that I'd read this past summer:
It did, however, remind me of another article that I'd read this past summer:
A water cloud containing the equivalent of 140 trillion times the water held in Earth's oceans has been detected around a quasar powered by a giant black hole 12 billion light years away.Note that this is water vapor, not liquid water or ice. Also note that this cloud is huge: it spans hundreds of lightyears around a supermassive black hole. Pretty cool.
Europa
Jupiter has 65 satellites, according to the Carnegie Institution for Science. They vary greatly (four of them make up almost all the mass, and Ganymede makes up a third of "almost all" by itself). It is these four, known as the Main Group or the Galilean Moons, that have captured the most interest, perhaps mostly because, as the largest, the are the easiest to see. They are known as the Galilean Moons because they were discovered in 1609 and 1610 by Galileo Galilei, who also famously recorded their orbits around Jupiter, bringing more support to the heliocentric view of the solar system.
As an aside, Galileo originally wanted to name the moons after the four brothers at the head of the powerful Medici family: Cosimo, Francesco, Carlo, and Lorenzo. This idea, though, proved to be less popular outside Florence, leading to the names we know today: Io, Ganymede, Europa, and Callisto, four lovers of the god Zeus in Greek mythology.
Europa, a Galilean moon and the sixth from Jupiter, is a bit smaller than Earth's moon, has a surface made up mostly of silicate rock, and probably has an iron core. It even has a thin atmosphere of oxygen. These and other geological features of the moon have led some to speculate that Europa holds large reserves of subterranean water, possibly entire oceans underground. Because of this, Europa is one of the leading candidates in the solar system for potential habitability and the presence of extraterrestrial life (well, at least since Mars let us down).
Which leads me into this new development. Geophysicists at UT Austin have possibly discovered a large (about the volume of the Great Lakes), surface lake of liquid water on Europa (and by surface, I of course mean several kilometers below the surface). The lake, like much of Europa's surface is mostly obscured by a thick ice shell, and it's not really known what is below it. A large subsurface ocean is one possibility, but another model claims that the top layer, composed of cold and brittle ice, covers a much thicker layer of warmer, convecting ice.
As far as I can tell, this new find doesn't necessarily support either model. This simulation of the formation of the lake seems to ignore that which lies far beneath the surface, instead showing how the lake can form just beneath the top ice sheet. It's possible, though, that I'm not interpreting this correctly.
This certainly isn't enough to get into the idea of actual life on Europa (though apparently some people have even been talking about colonizing it). Liquid water is, however, a step in that direction; it is also just interesting to learn more about the features of our solar system.
As an aside, Galileo originally wanted to name the moons after the four brothers at the head of the powerful Medici family: Cosimo, Francesco, Carlo, and Lorenzo. This idea, though, proved to be less popular outside Florence, leading to the names we know today: Io, Ganymede, Europa, and Callisto, four lovers of the god Zeus in Greek mythology.
Europa, a Galilean moon and the sixth from Jupiter, is a bit smaller than Earth's moon, has a surface made up mostly of silicate rock, and probably has an iron core. It even has a thin atmosphere of oxygen. These and other geological features of the moon have led some to speculate that Europa holds large reserves of subterranean water, possibly entire oceans underground. Because of this, Europa is one of the leading candidates in the solar system for potential habitability and the presence of extraterrestrial life (well, at least since Mars let us down).
Which leads me into this new development. Geophysicists at UT Austin have possibly discovered a large (about the volume of the Great Lakes), surface lake of liquid water on Europa (and by surface, I of course mean several kilometers below the surface). The lake, like much of Europa's surface is mostly obscured by a thick ice shell, and it's not really known what is below it. A large subsurface ocean is one possibility, but another model claims that the top layer, composed of cold and brittle ice, covers a much thicker layer of warmer, convecting ice.
As far as I can tell, this new find doesn't necessarily support either model. This simulation of the formation of the lake seems to ignore that which lies far beneath the surface, instead showing how the lake can form just beneath the top ice sheet. It's possible, though, that I'm not interpreting this correctly.
This certainly isn't enough to get into the idea of actual life on Europa (though apparently some people have even been talking about colonizing it). Liquid water is, however, a step in that direction; it is also just interesting to learn more about the features of our solar system.
Tuesday, November 15, 2011
Stars and the Virial Theorem
The Virial Theorem is a theorem in mechanics that relates the kinetic energy of particles in a system to the potential of the system. This can be useful when talking about stars, which balance both an immense gravitational collapsing force from their huge mass with the outward force from the internal particles heated from fusion at the star's core.
Sunday, November 13, 2011
Wednesday, November 9, 2011
Happy Birthday, Carl Sagan
Today would be Carl Sagan's 77th birthday. He was an American astronomer and popular science writer, known for such works as Cosmos, The Demon Haunted World, and the novel Contact, which was later adapted into a film. But my personal favorite book of his is Pale Blue Dot, from which the above speech was taken. He is referencing this picture:
 |
| Picture from www.realscience.us |
 |
| Picture from Wikipedia |
This one was taken by Apollo 8 crewmember Bill Anders, on December 24, 1968.
The Initial Mass Function II: The Luminosity Strikes Back
Continuing the problem from the previous post (and ignoring the lame Star Wars reference), we now have 3 mass categories of stars in the cluster, and the total masses contained in each of these categories in the cluster.
Now suppose we want to find the total luminosity of the cluster. If the luminosity scaled with mass the same way for all masses of stars, then this would be easy. We could just use the total mass and convert it to luminosity using that relation.
It's not quite that simple, though, which is why in the previous post it was necessary to break the stars into categories: different masses of stars have different mass-luminosity relations. Here they are for low, intermediate, and high mass stars, respectively:
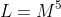
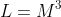
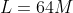
So, with each of the masses calculated in the previous post, we can use each of these relations to find the total luminosity for each category. The sum of these will be the total luminosity of the cluster.
I left those masses in terms of the solar mass, so finding the luminosity in erg/s will take some calculation. Help me, WolframAlpha, you are my only hope...
Once the luminosities are found, one can use them and Wien's Displacement Law to find the maximum-intensity wavelengths of the stars. Because younger stars are generally more luminous than older ones (they have more fuel which they use more wuickly), the average output radiation will be toward the blue end of the spectrum; older, cooler stars tend to be red.
Now suppose we want to find the total luminosity of the cluster. If the luminosity scaled with mass the same way for all masses of stars, then this would be easy. We could just use the total mass and convert it to luminosity using that relation.
It's not quite that simple, though, which is why in the previous post it was necessary to break the stars into categories: different masses of stars have different mass-luminosity relations. Here they are for low, intermediate, and high mass stars, respectively:
So, with each of the masses calculated in the previous post, we can use each of these relations to find the total luminosity for each category. The sum of these will be the total luminosity of the cluster.
I left those masses in terms of the solar mass, so finding the luminosity in erg/s will take some calculation. Help me, WolframAlpha, you are my only hope...
Once the luminosities are found, one can use them and Wien's Displacement Law to find the maximum-intensity wavelengths of the stars. Because younger stars are generally more luminous than older ones (they have more fuel which they use more wuickly), the average output radiation will be toward the blue end of the spectrum; older, cooler stars tend to be red.
Tuesday, November 8, 2011
The Initial Mass Function
The Initial Mass Function describes the mass distribution of a population of stars based on their theoretical initial masses (the masses they had at "birth"). The IMF is an empirically derived function; ie, it has been found to be true in numerous actual sets of stars, and was derived from that data, rather than being theoretically predicted. The IMF has this form:

where N is the number of stars, M is the mass of a star, and A is a proportionality constant.
Suppose we have discovered a newly formed globular cluster with a total mass of a million solar masses, and the masses of the stars it contains range from .1 solar masses to 20 solar masses. What can we find out about the cluster given this information?
First, we ought to find A. The first step is to integrate, so we have N as a function of M. (And we'll be playing a little fast and loose with the rules of differential equations, so don't hate me, mathematicians.)

from one tenth of a solar mass to 20 solar masses. Don't get too hung up on the limits of integration, because we'll be integrating again right away. This will give us the total mass of the system, which, fortunately, we know:
![\bg_white M_T=10^6M_S=\int NdM=\frac{-A}{1.35}\int_{.1M_S}^{20M_S}M^-^1^.^3^5dM=\frac{-A}{(1.35)(-.35)}[(\frac{1}{20M_S})^.^3^5-(\frac{1}{.1M_S})^.^3^5]](http://latex.codecogs.com/gif.latex?\bg_white M_T=10^6M_S=\int NdM=\frac{-A}{1.35}\int_{.1M_S}^{20M_S}M^-^1^.^3^5dM=\frac{-A}{(1.35)(-.35)}[(\frac{1}{20M_S})^.^3^5-(\frac{1}{.1M_S})^.^3^5])
Substituting in the values for the variables (and rounding a bit, and approximating), we get
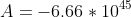
Cool. Now, suppose we divide the stars into categories: massive (between 8 and 20 solar masses), intermediate (between 1 and 8 solar masses) and low-mass (between .1 and 1 solar masses).What is the fraction of total stars in the cluster from each of these categories?
First, we can find the total number in each category. Now that we have the value of A, we can use the first integral above (where we found N as a function of M), except changing the limits of integration to be one of the sets of boundaries for a mass category (eg, 8 masses to 20 masses for massive stars). Solving these integrals gives around 3540 massive stars, 77,600 intermediate stars, and 1,767,000 low-mass stars. This makes massive stars about .2 % of the cluster by number, intermediate stars about 4.2 %, and low-mass stars 95.6 %.
One can also find the total mass contained in each of these categories in this particular cluster by using similar limits on the second integral. This gives about 75,000 solar masses; 280,000 solar masses; and 650,000 solar masses, respectively.
I will continue discussing the Initial Mass Function in a second post, covering more of this problem.
Worked out with Mee and David.
where N is the number of stars, M is the mass of a star, and A is a proportionality constant.
Suppose we have discovered a newly formed globular cluster with a total mass of a million solar masses, and the masses of the stars it contains range from .1 solar masses to 20 solar masses. What can we find out about the cluster given this information?
First, we ought to find A. The first step is to integrate, so we have N as a function of M. (And we'll be playing a little fast and loose with the rules of differential equations, so don't hate me, mathematicians.)
from one tenth of a solar mass to 20 solar masses. Don't get too hung up on the limits of integration, because we'll be integrating again right away. This will give us the total mass of the system, which, fortunately, we know:
Substituting in the values for the variables (and rounding a bit, and approximating), we get
Cool. Now, suppose we divide the stars into categories: massive (between 8 and 20 solar masses), intermediate (between 1 and 8 solar masses) and low-mass (between .1 and 1 solar masses).What is the fraction of total stars in the cluster from each of these categories?
First, we can find the total number in each category. Now that we have the value of A, we can use the first integral above (where we found N as a function of M), except changing the limits of integration to be one of the sets of boundaries for a mass category (eg, 8 masses to 20 masses for massive stars). Solving these integrals gives around 3540 massive stars, 77,600 intermediate stars, and 1,767,000 low-mass stars. This makes massive stars about .2 % of the cluster by number, intermediate stars about 4.2 %, and low-mass stars 95.6 %.
One can also find the total mass contained in each of these categories in this particular cluster by using similar limits on the second integral. This gives about 75,000 solar masses; 280,000 solar masses; and 650,000 solar masses, respectively.
I will continue discussing the Initial Mass Function in a second post, covering more of this problem.
Worked out with Mee and David.
Monday, November 7, 2011
Professional Astronomy
"The primary mission of our department is twofold: the performance of cutting-edge research in astronomy and astrophysics, including theory, observation, and experiment, as well as the education of undergraduate and graduate students and training of postdoctoral research associates who will comprise the scientists and leaders of tomorrow."This is how the Caltech Astronomy Department defines its purpose, as given on its website. This is, of course, a pretty broad definition, so it can include a lot of different people doing a lot of different things. Furthermore, the teaching faculty page breaks down the astrophysics faculty into theoretical, observational, and experimental astrophysicists; each may encompass a different aspect of what astronomers do (though the more literal-minded among us may consider only observational astrophysics to "really" be astronomy).
So, if one defines a professional astronomer as a person who has a faculty position in astrophysics, the above definition may be pretty sound. But this is not the only avenue for astronomy. For example, I did research this summer with scientists at the Spitzer Science Center. Though the Center is affiliated with and on the campus of Caltech, the people who do research there are not professors; they do not teach courses. So one can be an astronomer outside of (albeit still close to) academia.
The only astronomy research I am personally familiar with is observational. Last summer, as I've mentioned before, I used data from bright, infrared galaxies to draw conclusions about infrared power sources. And a year before that, I used photometry to calculate the rotational periods of asteroids. As a result, I don't really know much about the more theoretical side of astronomy. Learning more about that is one of my main goals for my time here at Caltech.
Subscribe to:
Comments (Atom)